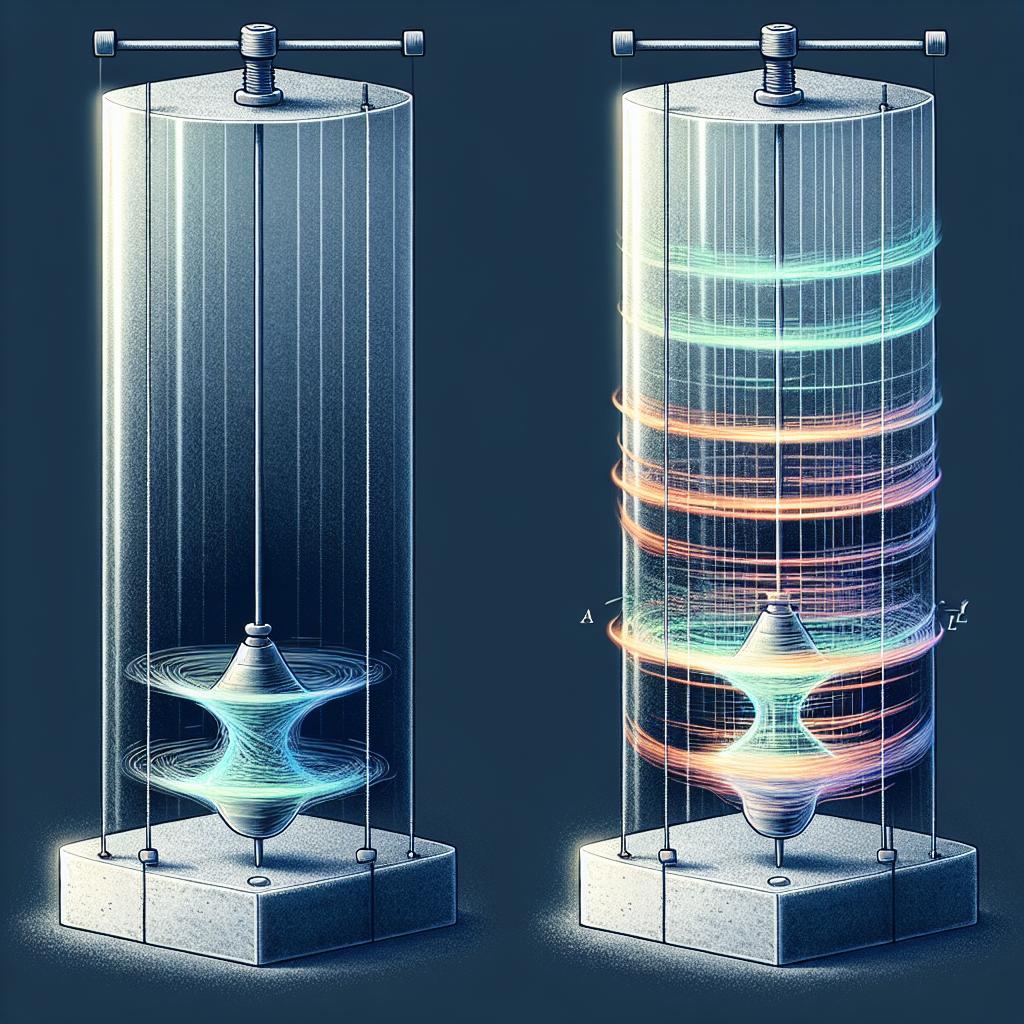
Ungedämpfte Schwingungen modellieren ideale, verlustfreie Systeme: konstante Amplitude, unveränderte Eigenfrequenz, scharfes Resonanzmaximum. Gedämpfte Schwingungen berücksichtigen Reibung: Amplitude fällt exponentiell, Eigenfrequenz verschiebt sich leicht, Resonanz verbreitert sich. In der Praxis dominiert Dämpfung zur Stabilität.