Ob Radioempfang, kontaktloses Bezahlen oder drahtloses Laden: Hinter vielen alltäglichen Technologien steckt ein unsichtbarer Dirigent namens Resonanz. Im Zentrum steht oft ein erstaunlich schlichtes Konstrukt – der Schwingkreis. Er ist das elektrische Pendant zum Pendel: Energie wandert rhythmisch hin und her, nicht zwischen Lage und Bewegung, sondern zwischen elektrischem Feld im Kondensator und magnetischem Feld in der Spule.
Dieser periodische Energieaustausch verleiht dem Schwingkreis seine Eigenfrequenz und sein selektives Gehör für bestimmte Töne des Frequenzspektrums. Reale Verluste dämpfen die Schwingung, die Güte bestimmt, wie scharf ein Schwingkreis „abstimmt”. In Varianten als Serien- oder Parallelschwingkreis wird er zum Filter, zum Tongeber, zur Frequenzlupe – und damit zum Grundbaustein unzähliger analoger und funkbasierten Anwendungen.
In diesem Artikel klären wir, was Schwingkreise sind, wie sie aufgebaut sind und warum sie schwingen. Wir ordnen die wichtigsten Kenngrößen ein, zeigen typische Schaltungen und werfen einen Blick auf Anwendungen von der Funktechnik bis zur Signalaufbereitung. So wird aus dem abstrakten Begriff ein greifbares Werkzeug – präzise, vielseitig und überraschend elegant.
Inhalte
- Was sind Schwingkreise und warum schwingen sie
- Bauteile im Zusammenspiel Kondensator Spule und Widerstand verständlich erklärt
- Eigenfrequenz Güte und Dämpfung vom Konzept zur Berechnung
- Resonanz in der Praxis Anwendungen von Filtern über Tuner bis Sensorik
- Designempfehlungen für stabile Schwingkreise Auswahl von Bauteilen Layout und Toleranzen
- Fehlerdiagnose und Optimierung typische Probleme messen interpretieren beheben
- Sicherheit und EMV im Umgang mit Schwingkreisen praktische Hinweise für Labor und Produkt
- FAQ
- Abschließende Bemerkungen

Was sind Schwingkreise und warum schwingen sie
Ein Schwingkreis ist ein elektrisches System, in dem sich elektrische und magnetische Energie periodisch austauschen. Herzstück sind eine Kapazität (C) und eine Induktivität (L)-der Kondensator speichert Energie im elektrischen Feld, die Spule im magnetischen Feld. Wird das System angestoßen, „pendelt” die Energie verlustarm zwischen C und L, vergleichbar mit einer Schaukel: einmal in Bewegung, trägt die Trägheit es weiter, bis Dämpfung es bremst.
| Bauteil | Rolle | Energieform |
|---|---|---|
| Kondensator (C) | Spannungsspeicher | Elektrisches Feld |
| Spule (L) | Stromspeicher | Magnetisches Feld |
Warum beginnt das System zu schwingen? Ein kurzer Impuls, eine Aufladung des Kondensators oder eine Stromänderung durch die Spule reicht: Der Kondensator entlädt sich durch L, der Strom baut ein Magnetfeld auf, dieses bricht wieder zusammen und lädt C um-die Polarität kehrt sich um, der Vorgang wiederholt sich. In einem idealen LC-Kreis wäre die Schwingung ungedämpft; in der Realität sorgen Widerstände für Verluste, die Amplitude klingt langsam aus. Die natürliche Eigenfrequenz hängt nur von L und C ab (Faustregel: f0 ≈ 1/(2π√(LC))); je größer L·C, desto tiefer der Ton.
- Anregung: kurzer Stoß, Rauschen oder eine Startladung.
- Austausch: C gibt Energie an L, L gibt sie an C zurück.
- Dämpfung: reale Verluste senken die Amplitude (R).
- Erhaltung: mit aktiver Verstärkung/Feedback bleibt die Schwingung dauerhaft.
Nützlich wird das Ganze, weil die Schwingung selektiv ist: Schwingkreise filtern Frequenzen, stimmen Radiosender ab, definieren Taktgeber und koppeln Energie bei drahtlosem Laden. Designer steuern das Verhalten über L, C und den Q‑Faktor (Verlustarmut). Höheres Q bedeutet schmalere Bandbreite und höhere Spannungsspitzen; Kopplung zu anderen Kreisen verschiebt und teilt Energie. So entsteht aus zwei einfachen Bauteilen ein präzises, fein abstimmbares Frequenzwerkzeug.
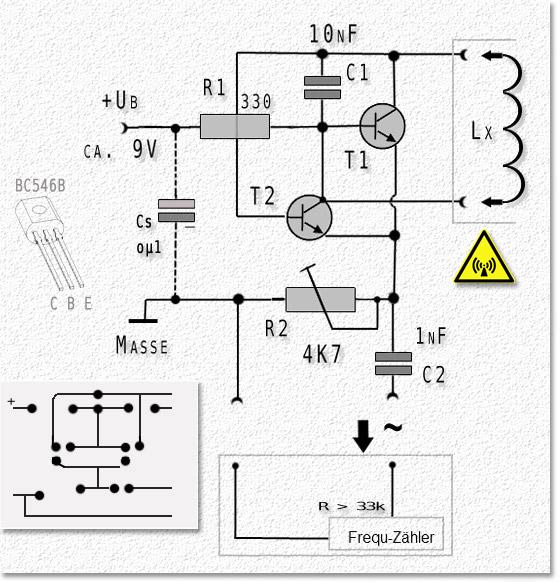
Bauteile im Zusammenspiel Kondensator Spule und Widerstand verständlich erklärt
Stell dir das Geschehen wie ein Ping-Pong der Energie vor: Der Kondensator speichert elektrische Ladung und Spannung, die Spule speichert Strom und ein Magnetfeld. Wenn der eine „leerläuft”, lädt der andere sich auf – hin und her, bis der Widerstand als Reibung mitmischt und einen Teil in Wärme verwandelt. Genau dieses Wechselspiel formt die Resonanz eines Schwingkreises: eine bevorzugte Frequenz, bei der das Energietauschen am intensivsten ist.
- Kondensator: speichert Ladung; mag schnelle Wechsel, blockiert Gleichstrom; bestimmt zusammen mit L die Schwingfrequenz.
- Spule: bremst Stromänderungen; bevorzugt langsame Wechsel; liefert das Magnetfeder-Gegenstück zum C.
- Widerstand: setzt die Dämpfung fest; je größer R, desto kleiner die Güte und desto breiter das Durchlassband.
- Zusammenspiel: C und L tauschen Energie, R legt fest, wie lange das „Nachschwingen” hör- bzw. messbar bleibt.
Entscheidend ist die Phasenverschiebung: In der Spule hinkt der Strom der Spannung hinterher, im Kondensator eilt er voraus – dadurch können sich Wirkungen aufheben oder verstärken. Bei Resonanz gleichen sich die Blindanteile von C und L aus; übrig bleibt die Wirkung von R, der die Kurve flacher oder schärfer macht. So lässt sich ein Schwingkreis als Filter abstimmen: scharf und selektiv (hohe Q) oder breitbandig und robust (niedrige Q).
| Änderung | Resonanz f0 | Güte Q | Bandbreite | Kurznotiz |
|---|---|---|---|---|
| C ↑ | ↓ | ↓ | ↑ | tiefer, weicher |
| L ↑ | ↓ | ↑ | ↓ | tiefer, schärfer |
| R ↑ | ≈ | ↓ | ↑ | stärker gedämpft |
Praktisch heißt das: Mit mehr C oder L verschiebst du die Tonlage der Resonanz, mit R stellst du ein, wie „klingend” oder „trocken” das Ergebnis ist. Tuner in Radios gewinnen ihre Selektivität aus hoher Q (kleiner R, geeignete L/C), während Sensoren und Dämpfungsglieder bewusst R erhöhen, um Störungen zu glätten. Kleine Änderungen an nur einem Bauteil können den ganzen Charakter des Schwingkreises spürbar drehen.
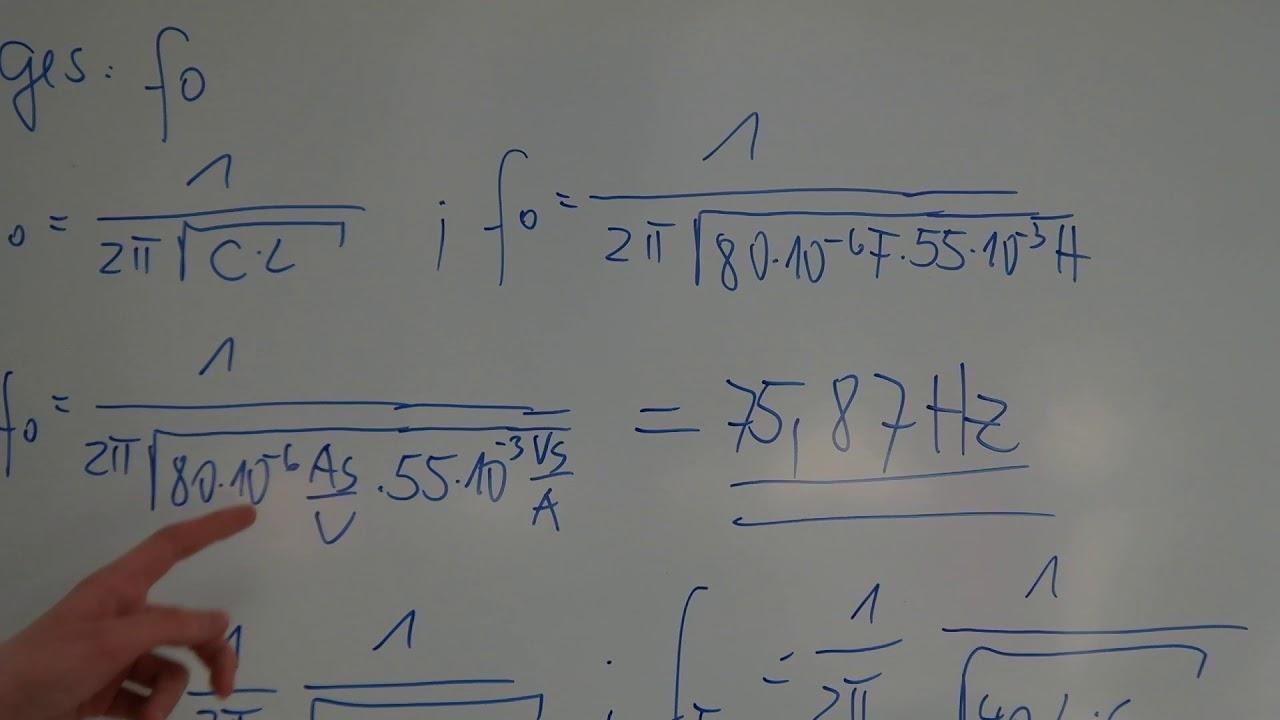
Eigenfrequenz Güte und Dämpfung vom Konzept zur Berechnung
Resonanz in einem RLC-System entsteht, wenn sich Energie zyklisch zwischen Induktivität und Kapazität austauscht, während der ohmsche Anteil kontinuierlich Energie abbaut. Die charakteristische Frequenz ergibt sich idealisiert zu f₀ = 1 / (2π√(LC)) und bestimmt, wo maximale Spannungs- oder Stromüberhöhung auftritt. In der Praxis verschieben parasitäre Widerstände, Wicklungsverluste und Dielektrika diesen Punkt geringfügig und beeinflussen die Schärfe der Kurve.
- C ↑ → f₀ sinkt, Energie liegt stärker im elektrischen Feld.
- L ↑ → f₀ sinkt, Energie liegt stärker im magnetischen Feld.
- R ↗ → geringere Selektivität, schnellere Abklingzeit.
Die Güte Q beschreibt die Selektivität (schmale Bandbreite, hohe Überhöhung), das Dämpfungsmaß ζ den Abklingcharakter. Für den Serienfall gilt typischerweise Q = ω₀L/R und ζ = R/(2)·√(C/L); im Parallelfall entsprechend Q = R/(ω₀L) und ζ = (1/(2R))·√(L/C). Mit ω₀ = 1/√(LC) und Δf = f₀/Q lässt sich die Bandbreite direkt aus der Zielgüte bestimmen. Werte von ζ < 1 bedeuten unterkritische Dämpfung (schwingfähig), ζ = 1 kritische Dämpfung und ζ > 1 Überdämpfung.
| Größe | Serie RLC | Parallel RLC | Einheit |
|---|---|---|---|
| ω₀ | 1/√(LC) | rad/s | |
| f₀ | 1/(2π√(LC)) | Hz | |
| Q | ω₀L/R = 1/(ω₀RC) | R/(ω₀L) = ω₀RC | – |
| ζ | (R/2)·√(C/L) | (1/(2R))·√(L/C) | – |
| Δf | f₀/Q | Hz | |
Vom Entwurf zur Rechnung: Starten Sie mit Ziel-Frequenz und gewünschter Bandbreite oder Güte, wählen Sie die Topologie passend zur Quelle/Last und dimensionieren Sie Bauteile mit kompakten Formeln. Ein typischer Ablauf: L oder C pragmatisch setzen (Verfügbarkeit, ESR), das Gegenstück über C = 1/((2πf₀)²·L) ermitteln und anschließend den Widerstand so wählen, dass Q und ζ treffen. Vergessen Sie nicht reale Verluste (ESR/ESL), Toleranzen und den Einfluss der Kopplung zu berücksichtigen.
- Serie: R = ω₀L/Q = 1/(ω₀CQ)
- Parallel: R = Q·ω₀L = Q/(ω₀C)
- Praxistipp: Messbare Q ist häufig geringer als berechnet → Sicherheitsmargen einplanen.

Resonanz in der Praxis Anwendungen von Filtern über Tuner bis Sensorik
Filter verwandeln das schwingfähige Zusammenspiel von L und C in messerscharfe Auswahl: Die Resonanzfrequenz definiert das Durchlassfenster, die Güte (Q) die Kantensteile, und die Dämpfung legt die Bandbreite fest. Ob als schmalbandiger Bandpass in Empfängervorstufen oder als Kerbfilter gegen Störträger – ein gezielt dimensionierter RLC-Zweig wirkt wie eine Frequenz-Lupe, die Nutzsignale hervorhebt und Rauschen seitlich abblendet.
- HF-/RF-Filter: Vorselektion, Störerunterdrückung, Schutz vor Intermodulation
- Audio: Frequenzweichen, Notch gegen Netzbrummen
- Antennentuning: SWR-Optimierung, Reichweitengewinn
- Oszillatoren: VCO, PLL-Referenz, Frequenzsynthese
- Sensorik: induktiv (Näherung), kapazitiv (Feuchte), resonant (Mikrowaage)
Für Tuner und Matching-Netzwerke wird Resonanz zum verstellbaren Werkzeug: Varaktor– oder MEMS-Kapazitäten schieben die Eigenfrequenz, PLL und DDS referenzieren oder synthetisieren darauf basierend stabile Kanäle, und der Antennentuner maximiert die Kopplung im Zielband. Aus derselben Topologie entsteht so ein präziser Frequenz-Drehknopf – vom UKW-Front-End bis zum IoT-Transceiver.
| Anwendung | Resonanzelement | Abstimmung | Nutzen |
|---|---|---|---|
| Bandpass-Filter | LC parallel | fest | Selektivität |
| Antennentuner | LC Serie | variabel | Leistungsanpassung |
| VCO | LC + Varaktor | spannungsgesteuert | Frequenzwahl |
| Induktiver Sensor | RLC parallel | medienabhängig | Kontaktlose Messung |
In der Sensorik wird die Messgröße selbst zum Tuning-Knopf des Schwingkreises: Änderungen von Kapazität, Induktivität oder Verlusten verschieben die Frequenz oder senken den Q-Faktor. Induktive Wirksensoren detektieren Metalle via Wirbelströme, kapazitive Aufnehmer erfassen Permittivitätsänderungen, und Quarz– bzw. SAW-Resonatoren registrieren Massenbeläge in ppm – energiearm, oft kontaktlos und hochstabil.

Designempfehlungen für stabile Schwingkreise Auswahl von Bauteilen Layout und Toleranzen
Bauteilauswahl entscheidet über Stabilität und Güte: Für Kapazitäten bevorzugen sich temperaturstabile Dielektrika wie NP0/C0G (geringe Drift, niedrige Verluste) gegenüber X7R/Y5V in resonanzkritischen Zweigen. Achten Sie bei Induktivitäten auf hohen Q-Faktor, niedrige ESR und eine Selbstresonanzfrequenz (SRF), die deutlich über der Zielresonanz liegt. Der Sättigungsstrom des L darf im Betrieb nicht erreicht werden; sonst verschiebt sich die Resonanz. Für abstimmbare Kreise sind Trimmer-Cs oder Varaktordioden mit geringem Leckstrom und gut dokumentierter Kennlinie empfehlenswert. SMD-Bauteile minimieren parasitäre Induktivitäten; wo nötig, sichern eng tolerierte Typen (z. B. ±1…2 %) die Reproduzierbarkeit.
- Cap-Tipp: NP0/C0G (±1…5 %) für den resonanzbestimmenden Pfad, X7R nur für unkritische Entkopplung.
- Inductor-Tipp: Q ≥ 30 am Arbeitspunkt, SRF ≥ 3× f0, abgeschirmte Bauform gegen Streufelder.
- Verluste niedrig halten: ESR-Datenblattkurven bei f0 prüfen; Gehäusegröße nicht zu klein wählen.
- Abgleich vorsehen: Trimmer-C im Bereich 2…10 pF oder selektierbare C‑Arrays für Serienfertigung.
Layout prägt den Kreis – der Rückstromweg zählt: Halten Sie die Schleifenfläche von L und C minimal und platzieren Sie die Bauteile eng beieinander auf einer durchgehenden Massefläche. Vermeiden Sie Parallelführung neben Takt- oder Leistungsleitungen; richten Sie benachbarte Induktivitäten um 90° versetzt aus, um magnetische Kopplung zu reduzieren. Nutzen Sie Via‑Stitching als Schirmzaun, definieren Sie „Keep‑out”-Zonen und bewahren Sie Symmetrie bei differenziellen Strukturen. Für HF gilt: kurze, breite Leiter, gleichmäßige Impedanz, und Mess-/Abgleichpunkte so platzieren, dass die Kreisgüte beim Kontakt nicht kollabiert.
| Layout-Regel | Warum | Schnelltest |
|---|---|---|
| Loop kurz & kompakt | Weniger parasitäre L/R | Fläche < 1 cm² (HF) |
| Durchgehende Masse | Stabiler Rückweg | Keine Splits unter L/C |
| 90° L‑Orientierung | Geringere Kopplung | Q fällt nicht nebenan |
| Via‑Fence | Abschirmung | Pitch ~1/20 λ |
| Abgleichzugang | Serien‑Tuning | Pad für Trimmer/Netzwerk |
Toleranzen beherrschen, Drift einkalkulieren: Legen Sie eine Toleranzbilanz an (Bauteil‑Toleranz, Temperaturkoeffizient, Alterung, Montageparasitiken) und prüfen Sie die Resonanzverschiebung über f0 = 1/(2π√(LC)). Planen Sie für Produktion eine Abgleichreserve von 5…10 % in C oder L ein und definieren Sie Grenzwerte für Q und Einfügedämpfung. Nutzen Sie Monte‑Carlo‑Simulationen mit realistischen ESR/SRF‑Modellen; berücksichtigen Sie Temperaturdrifts (z. B. C0G ~ ±30 ppm/°C, Ferrit‑Kerne deutlich höher). Für robuste Serienergebnisse helfen: Selektieren kritischer Bauteile, Derating beim Strom, feuchte‑ und vibrationsarme Platzierung sowie dokumentierte Prüfpunkte für schnellen End‑of‑Line‑Abgleich.
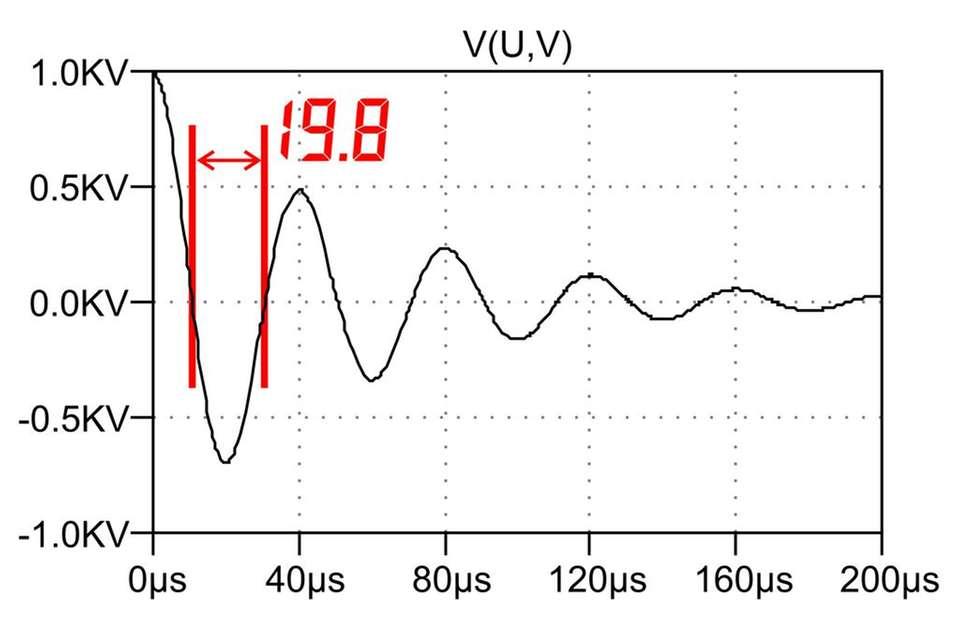
Fehlerdiagnose und Optimierung typische Probleme messen interpretieren beheben
In realen LC-Schwingkreisen treten Abweichungen auf, die sich als verschobene Resonanz, verringerte Güte oder unerwartete Nebenmaxima zeigen. Häufige Auslöser sind Bauteiltoleranzen (z. B. ±10 % bei Standard-C), parasitäre Widerstände/Induktivitäten (ESR/ESL), Belastung durch Messspitzen oder angeschlossene Stufen, sowie Kopplungen zu benachbarten Leiterzügen oder Metallflächen. Auch Temperaturdrift und Kernsättigung bei höheren Anregungspegeln verschieben die Eigenfrequenz und drücken die Güte (Q). Ein sauberer Aufbau, kurze Leitungen und das bewusste Führen von Rückströmen sind entscheidend, um das „ideale” Verhalten aus dem Lehrbuch zu erreichen.
- Resonanz verschoben: Toleranzen, parasitäre Kapazitäten/Induktivitäten, thermische Effekte.
- Breiter, flacher Peak: Hoher ESR, Last zu niederohmig, schlechte Abschirmung.
- Doppelte oder gezackte Peaks: Gekoppelte Moden, Schleifenfläche zu groß, Nachbarsignale.
- Amplitude abhängig vom Anregungspegel: Kernsättigung, nichtlinearer Dielektrikumverlust.
- Kurzes Ausschwingen: Übermäßige Dämpfung durch ESR, Messaufbau oder Dämpfungsglieder.
Für die Messung und Interpretation eignen sich LCR-Meter (Klein-Signal-Parameter), Frequenzgangmessung mit Generator und Oszilloskop/VNA (Bode-Plot), sowie Ausschwingmessungen per Impulsanregung. Achten Sie auf niedrige Messkapazität der Tastköpfe (10x/aktive Probe), saubere 50-Ohm-Abschlüsse und kurze, koaxiale Verbindungen. Aus dem Resonanzmaximum/-minimum lässt sich f0 bestimmen, aus der -3-dB-Bandbreite der Q-Faktor. Ein asymmetrischer Peak weist oft auf Belastung oder Nichtlinearitäten hin; ein Doppelpeak deutet auf unerwünschte Kopplung mehrerer Resonanzen. Prüfen Sie Messpegel, um Pegelabhängigkeit (Sättigung) zu erkennen, und vergleichen Sie die Kurvenform mit einem Referenzaufbau.
| Messung | Muster | Ursache | Sofortmaßnahme |
|---|---|---|---|
| LCR (ESR/Q) | ESR höher als erwartet | Bauteilqualität, Temperatur | Low-ESR-C wählen, selektieren |
| Sweep (S21) | Breiter, niedriger Peak | Parasitärer R, Last | Quelle/Last anpassen, Leitungen verkürzen |
| Sweep (S21/S11) | Doppelpeak/Schulter | Kopplung, zweite Mode | Abstand erhöhen, schirmen, Layout entflechten |
| Puls-Ringdown | Schnelles Abklingen | Überdämpfung | ESR senken, Dämpfer überprüfen |
| Pegeltest | f0 wandert mit Pegel | Kernsättigung | Strom reduzieren, größerer/anderer Kern |
| Sweep (Notch) | Notch zu flach | Zu geringe Q, Leckpfade | PFAD schirmen, Dielektrikum C0G/NP0 |
Zur Behebung und Optimierung kombinieren Sie Bauteilauswahl, Layout und gezielte Dämpfung. Wählen Sie für Kondensatoren C0G/NP0 oder Silberglimmer, für Spulen einen Kern mit niedrigen Verlusten und ausreichender Sättigungsreserve; behalten Sie Q und ESR im Datenblatt im Blick. Minimieren Sie Schleifenflächen, nutzen Sie eine ruhige Masse, Via-Stitching und ggf. Schirmbleche. Führen Sie die Resonanz fein über Trimmer oder Varikaps nach und stabilisieren Sie die Bandbreite mit kleinen Serienwiderständen (kontrollierte Dämpfung). Stimmen Sie Quelle/Last ab, entkoppeln Sie benachbarte Stufen (Puffer, Ferrit), und reduzieren Sie Messartefakte mit niedriger Lastkapazität. So werden Resonanzfrequenz, Güte und Stabilität reproduzierbar – auch außerhalb des Labors.
- Bauteile: C0G/NP0, Luftspulen/geeignete Ferrite, enge Toleranzen.
- Layout: Kurze Verbindungen, kompakte Schleifen, saubere Masseführung.
- Tuning: Trimmer/Varikap, Serien-R zur Q-Kontrolle, Temperaturkompensation.
- Entkopplung: Abstand, Schirmung, Ferritperlen gegen Kopplungen.
- Messdisziplin: 50-Ohm-Umgebung, kalibrierte Pegel, kapazitätsarme Tastung.

Sicherheit und EMV im Umgang mit Schwingkreisen praktische Hinweise für Labor und Produkt
Resonanzkreise wirken wie Energiefallen: Schon kleine Anregungen können am Resonanzpunkt zu sehr hohen Spannungen oder Strömen führen. Planen Sie von Beginn an mit Strombegrenzung, Bleeder-Widerständen an Kondensatoren und klaren Abstands- und Isolationsregeln. Achten Sie auf heiße Ferrite, kapazitive Einkopplung über Messleitungen und auf das Nachschwingen beim Abschalten. Wer berührt oder kurzschließt, testet nicht – er riskiert Schäden. Prüfen Sie deshalb vor jedem Einschalten: Energiepfade, Entlademöglichkeiten und Messaufbau.
- Netzteil: Stromlimit setzen, sanft anfahren, Not-Aus griffbereit.
- Entladung: Fest verbauter Bleeder; bei Bedarf externer Widerstand mit isolierten Klemmen.
- Abstand: Finger- und Werkzeugsicherheit; scharfe Kanten und Lötspitzen abdecken.
- Messung: Hochspannungstastkopf, Stromzange; kurze Massefeder statt langer Tastkopf-Masseleitung.
- Thermik: IR-Kamera oder Thermosensor; Q gezielt dämpfen, wenn Bauteile heiß werden.
- HF-Hygiene: Nichtleitende Werkzeuge, geerdete Unterlage, klare Kabelwege.
Elektromagnetische Verträglichkeit beginnt beim Aufbau: Minimieren Sie Schleifenflächen, führen Sie stromrückführende Wege dicht am Hinleiter und verwenden Sie abgeschirmte oder verdrillte Leitungen. Dämpfung (Serienwiderstand, RC-Snubber) zähmt das Q und reduziert Abstrahlung. Für die Verifikation eignen sich Nahfeldsonden, Stromzangen am Versorgungsleiter und ein Spektrumanalysator. Denken Sie an Gleichtakt– versus Differenz-ströme: Filter und Schirmung wirken nur, wenn Bezugspunkte und Masseführung konsequent geplant sind.
| Problem | Ursache | Sofortmaßnahme |
|---|---|---|
| Überspannung am Peak | Hoher Q, geringe Last | Serien-R, Snubber, Last zuschalten |
| HF-Verbrennung | Kontakt an heißem Knoten | Abschirmung, isolierte Halter |
| ESD-Schaden | Labile Gate-/PN-Übergänge | ESD-Armband, TVS, Erdung |
| Abstrahlung | Große Schleifen, Leitungen | Twisten, Schirmen, Ferrite |
| Einkopplung | Gemeinsame Masse | Sternmasse, Trennung CM/DM |
Wird aus dem Versuchsaufbau ein Produkt, zählen Wiederholbarkeit und Nachweisbarkeit: Dokumentieren Sie Massekonzept, Filtertopologien (LC, CM-Drosseln), Gehäuseschirmung (nahtlose Fugen, leitfähige Dichtungen) und Kriech-/Luftstrecken. Planen Sie Pre-Compliance-Tests zu EN 55032/55011 (Emission) und EN 61000-4-2/-3/-4-6 (Immunität) ein. Definieren Sie Prüfadapter, sichere Testpunkte und mechanische Fixierung gegen Verstimmung. Wo nötig, reduzieren Sie das Q bewusst – lieber etwas Verlustleistung als Grenzwertüberschreitung.
- Design-Checks: Sternförmige Rückführung, kurze Schleifen, durchdachte Schirmanschlüsse beid- oder einseitig je Kopplungsweg.
- Filterung: Speisung nahe Quelle entkoppeln, Durchführkondensatoren an Gehäusedurchbrüchen.
- Sicherheit: Berührschutz, definierte Entladezeit, klare Kennzeichnung von Hotspots.
- Validierung: Nahfeldscan, Leitungsstrommessung, Störfestigkeits-Sweeps mit protokollierten Betriebszuständen.
- Wartung: Zugang nur im stromlosen Zustand; Entladehinweis und Prüfpunkte mit Schutzabdeckung.
FAQ
Frage: Was ist ein Schwingkreis?
Antwort: Ein Schwingkreis ist eine elektrische Anordnung, in der Energie periodisch zwischen einem elektrischen Feld (Kondensator) und einem magnetischen Feld (Spule) hin- und herpendelt. Idealerweise entstehen so sinusförmige Schwingungen.
Frage: Woraus besteht er typischerweise?
Antwort: Aus einer Induktivität L (Spule) und einer Kapazität C (Kondensator). In der Praxis ist immer auch ein Widerstand R vorhanden, der die Schwingung dämpft. Man spricht dann von einem RLC-Schwingkreis.
Frage: Wie startet eine Schwingung?
Antwort: Durch eine Anfangsbedingung (z. B. aufgeladener Kondensator) oder eine Anregung von außen (Wechselspannung). Ohne Verluste würde die Schwingung ewig laufen, reale Verluste lassen sie abklingen.
Frage: Was ist die Resonanzfrequenz?
Antwort: Die Frequenz, bei der sich die Blindanteile von L und C ausgleichen. Für einen idealen LC-Kreis gilt:
f0 = 1 / (2π√(LC))
mit L in Henry, C in Farad, f0 in Hertz.
Frage: Kleines Beispiel?
Antwort: L = 10 µH, C = 100 nF → LC = 1e−12, √(LC) = 1e−6, f0 ≈ 1 / (2π·1e−6) ≈ 159 kHz.
Frage: Was bedeutet der Gütefaktor Q?
Antwort: Q beschreibt, wie “verlustarm” der Schwingkreis ist. Er ist das Verhältnis gespeicherter Energie zu pro Periode verlorener Energie und bestimmt die Selektivität: Q ≈ f0 / Δf (Δf: −3 dB-Bandbreite). Für einen Serienkreis gilt näherungsweise Q = ω0L / R, für einen Parallelkreis Q = 1 / (ω0CR).
Frage: Was unterscheidet Serien- und Parallelschwingkreis?
Antwort: Beim Serienkreis ist die Impedanz bei Resonanz minimal (Strommaximum). Beim Parallelschwingkreis ist die Impedanz bei Resonanz maximal (Stromminimum von außen, Spannungsmaximum am Kreis).
Frage: Was ist der Unterschied zwischen freier und erzwungener Schwingung?
Antwort: Freie Schwingung läuft nach einer Anfangsenergie ab und klingt ab (Klingeln). Erzwungene Schwingung entsteht durch einen äußeren Antrieb; nahe der Resonanz wird die Amplitude groß, begrenzt durch Verluste und Nichtlinearitäten.
Frage: Welche Rolle spielt der Widerstand R?
Antwort: R dämpft die Schwingung, vergrößert die Bandbreite und senkt Q. Zu hohe Dämpfung unterdrückt Resonanzeffekte; zu geringe Dämpfung führt zu hoher Spannungs- oder Stromüberhöhung.
Frage: Wie verhalten sich Phasen bei Resonanz?
Antwort: Der Spannungsabfall an L eilt dem Strom um +90° voraus, an C eilt er um −90° nach. Bei Resonanz heben sich diese Blindanteile ideal auf; die Gesamtphase des Serienkreises ist dann 0°.
Frage: Wofür werden Schwingkreise verwendet?
Antwort: Unter anderem für:
– Radioempfang und -sender (Abstimmung, Filter)
– Oszillatoren (Frequenzbestimmung)
– RFID/NFC- und drahtlose Energieübertragung (gekoppelte Resonatoren)
– Frequenzselektive Verstärker, Zwischengleichungsfilter, EMV-Filter
– Quarzoszillatoren und MEMS-Resonatoren (mechanisch-elektrische Analogien)
Frage: Was sind gekoppelte Schwingkreise?
Antwort: Zwei oder mehr Schwingkreise, die magnetisch oder elektrisch gekoppelt sind. Sie bilden gemeinsame Eigenmoden, können Bandfilter realisieren und zeigen bei stärkerer Kopplung aufgespaltene Resonanzspitzen.
Frage: Welche Nichtidealitäten sind wichtig?
Antwort: Parasitärkapazitäten und -induktivitäten, ESR der Kondensatoren, Draht- und Kernverluste, Haut- und Proximity-Effekt, Toleranzen und Temperaturkoeffizienten. Sie verschieben f0 und senken Q.
Frage: Wie kann man Resonanzfrequenz und Q messen?
Antwort: Mit einem Netzwerkanalysator (S11/Impedanzverlauf), einem Sweepgenerator und Oszilloskop (Amplitude/Phase über Frequenz), oder einem LCR-Meter für Einzelbauteile. Bandbreite zwischen −3 dB-Punkten liefert Q.
Frage: Wie stimmt man einen Schwingkreis ab?
Antwort: Durch veränderliche Kapazitäten (Trimmkondensator, Varaktordiode) oder variable Induktivität (Ferritkern). Auch Feintuning über die Kopplung zu benachbarten Stufen ist üblich.
Frage: Ist Resonanz “gefährlich”?
Antwort: Sie kann hohe Spannungen oder Ströme im Kreis erzeugen, besonders bei hoher Q und starker Anregung. Bauteilgrenzen, Isolation, Kühlung und Sicherheitsabstände sind zu beachten.
Frage: Gibt es eine anschauliche Analogie?
Antwort: Ja, Masse-Feder-Dämpfer. Die Masse entspricht L, die Feder C (genauer: 1/C), und der Dämpfer R. Resonanzfrequenz, Güte und Abklingverhalten haben direkte Entsprechungen.
Frage: Warum Schwingkreise, wenn es digitale Filter gibt?
Antwort: Schwingkreise sind passiv, rauscharmer, energieeffizient, hochfrequenztauglich und können sehr hochselektive, stabile Referenzen bilden (z. B. Quarz). Digitale Lösungen bieten Flexibilität, aber erfordern Abtastung und Wandler.
Frage: Häufige Missverständnisse?
Antwort: Resonanz bedeutet nicht “unendliche” Energie, sondern eine Verstärkung begrenzt durch Verluste und Nichtlinearitäten. Außerdem ist “die” Resonanzfrequenz temperatur- und toleranzabhängig und kann durch Kopplung oder Last verschoben werden.
Frage: Praktische Tipps für den Aufbau?
Antwort: Kurze Leiterwege, gute Masseführung, abgeschirmte oder HF-taugliche Bauteile, C0G/NP0-Kondensatoren für Stabilität, geeignete Kerne für hohe Q, sorgfältige Kopplung und Lastanpassung, sowie Messpunkte mit minimaler Störung des Kreises.
Abschließende Bemerkungen
Schwingkreise sind mehr als ein Lehrbuchbeispiel: In ihnen tauschen elektrisches und magnetisches Feld Energie aus, bestimmt von L und C, gebremst durch Verluste und geprägt von Resonanz und Güte. Aus diesem einfachen Prinzip entstehen Filter, Tuner, Oszillatoren und drahtlose Schnittstellen – vom Radiotuner bis zur Induktivladung.
Wesentlich ist dabei die Differenz zwischen Ideal und Praxis: Bauteiltoleranzen, Temperaturdrift und parasitäre Elemente verschieben die Resonanz und verändern die Dämpfung. Wer Schwingkreise entwirft, arbeitet daher mit Simulation, Messung und sorgfältiger Dimensionierung – und gewinnt Stabilität, Selektivität und Effizienz.
Ob als Denkmodell oder als präzises Werkzeug: Der Schwingkreis liefert eine klare Sprache, um Frequenzen zu formen. Wer weitergeht, untersucht gekoppelte Kreise, nichtlineare Effekte oder aktive Kompensation – und lernt, wie aus einem einfachen LC-Pendel ein fein abgestimmtes System wird.